Assalammualaikum wr. wb.
My name is Yogi Kasbani, class XII IPA 7 SMAN 1 Teluk Jambe. This time I get an task from my physics teacher to create an article. I'm getting a discussion of the material the Longitudinal waves. Well I will start my interesting discussion and may good to read, and of course get good score from my physics teacher. Hehehe ... (^ _ ^)
{---LONGITUDINAL WAVES---}
Waves are vibratory disturbances traveling in a medium. If you
understand that sentence, you have understood wave motion. You are shown
vibrating layers of air in a horizontal tube. The layer at the extreme
left is the one disturbed earliest. A vibrating piston at the left end
is causing these disturbances. So the layer at the left extreme is
always ahead in phase of the layers to its right. The time lag between
the moments when different layers begin oscillating causes the layers to
come closer to each other at some moments and move farther at some
other moments. To get a feel of this, imagine what would have happened
if all the layers vibrated in phase. You would always have layers
maintaining the same distance between themselves and you would not have
any wave disturbance traveling in the medium. The key to understanding
of wave motion is this simple idea that phase is different for the
different vibrating particles because they start vibrating at different
times. The ones farther from the source oscillating later than the ones
closer to the source.

Longitudinal waves, also known as "l-waves", are waves that have
the same direction of vibration as their direction of travel, which
means that the movement of the medium is in the same direction as or the
opposite direction to the motion of the wave. Mechanical longitudinal
waves have been also referred to as compressional waves or compression waves.
Longitudinal waves include sound waves (alternation in pressure,
particle displacement, or particle velocity propagated in an elastic
material) and seismic P-waves (created by earthquakes and explosions).
Sound waves
In the case of longitudinal harmonic sound waves, the frequency and wavelength can be described with the formula
 |
| Longitudinal Waves |
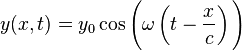
where:
y is the displacement of the point on the traveling sound wave;
x is the distance the point has traveled from the wave's source;
t is the time elapsed;
y0 is the amplitude of the oscillations,
c is the speed of the wave; and
ω is the angular frequency of the wave.
The quantity x/c is the time that the wave takes to travel the distance x.
The ordinary frequency (f) of the wave is given by
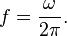
For sound waves, the amplitude of the wave is the difference between
the pressure of the undisturbed air and the maximum pressure caused by
the wave.
Sound's propagation speed depends on the type, temperature, and composition of the medium through which it propagates.
Pressure waves
 |
| Plane Pressure Pulse Waves |
In an elastic medium with rigidity, a harmonic pressure wave
oscillation has the form,

where:
- y0 is the amplitude of displacement,
- k is the wavenumber,
- x is distance along the axis of propagation,
- ω is angular frequency,
- t is time, and
 |
| pulse wave on 2d grid |
|
- φ is phase difference.
The force acting to return the medium to its original position is
provided by the medium's bulk modulus.
{---Longitudinal Mode---}
Now I will discuss about the longitudinal waves. Please Enjoy it.... (>_<)"
A longitudinal mode of a resonant cavity is a particular standing wave pattern formed by waves confined in the cavity. The longitudinal modes correspond to the wavelength of the wave which are reinforced by constructive interferance after many reflections from the cavity's reflecting surfaces. All other wavelengths are suppressed by destructive interference.
A longitudinal mode pattern has its nodes located axially along the length of the cavity. Transverse modes, with nodes located perpendicular to the axis of the cavity, may also exist.
 |
| six longitudinal modes of plane parallel cavity |
Simple cavity
A common example of longitudinal modes are the light wavelengths produced by a laser. In the simplest case, the laser's optical cavity is formed by two opposed plane (flat) mirrors surrounding the gain medium (a plane-parallel or Fabry-Perot cavity). The allowed modes of the cavity are those where the mirror separation distance L is equal to an exact multiple of half the wavelength, λ:
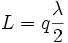
where q is an integer known as the mode order.
In practice, the separation distance of the mirrors L is usually much greater than the wavelength of light λ, so the relevant values of q are large (around 105 to 106). The frequency separation between any two adjacent modes, q and q+1, in a material that is transparent at the laser wavelength, are given (for an empty linear resonator of length L) by Δν:
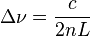
where c is the speed of light and n is the refractive index of the material (note: n=1 in air).
Composite cavity
If the cavity is non-empty (i.e. contains one or more elements with different values of refractive index), the values of L used are the optical path lengths for each element. The frequency spacing of longitudinal modes in the cavity is then given by:
![\Delta \nu = \frac{c}{2\sum_i n_i L_i} = \frac{c}{2}\left[ \frac{1}{n_1 L_1 + n_2 L_2 + n_3 L_3 + \ldots} \right]](https://upload.wikimedia.org/wikipedia/en/math/3/a/8/3a8e58d7f5f3c138c779d552935bfd87.png)
where ni is the refractive index of the i'th element of length Li.
More generally, the longitudinal modes may be found for any type of wave in a cavity by solving the relevant wave equation with the appropriate boundary conditions.
Both transverse and longitudinal waves may have longitudinal modes when confined to a cavity.
The analysis of longitudinal modes is especially important in lasers with single transversal mode, for example, in single-mode fiber lasers.
The number of longitudinal modes of such a laser can be estimated as
ratio of the spectral width of gain to the spectral separation of
longitudinal modes.
Power per longitudinal mode
For lasers with single transversal mode, the power per one longitudinal mode can be significantly increased by the coherent addition
of lasers. Such addition allows one to both scale-up the output power
of a single-transverse-mode laser and reduce number of longitudinal
modes, because the system chooses automatically only the modes which are
common for all the combined lasers. The reduction of the number of
longitudinal modes determines the limits of the coherent addition.
The ability to coherently add one additional laser is exhausted when
one longitudinal mode, common for the combined lasers, lies within the
spectral width of the gain, a subsequent addition will lead to loss of
efficiency of the coherent combination and will not increase the power
per longitudinal mode of such a guitar strings.
 |
| Guitar Strings is Longitudinal Waves |
Well ... so that I can give the task of physics article about this longitudinal waves ....
I hope to do well .... hehehe ....
Wassalammualaikum wr. wb.







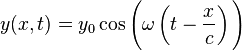
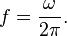

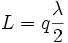
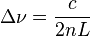
![\Delta \nu = \frac{c}{2\sum_i n_i L_i} = \frac{c}{2}\left[ \frac{1}{n_1 L_1 + n_2 L_2 + n_3 L_3 + \ldots} \right]](https://upload.wikimedia.org/wikipedia/en/math/3/a/8/3a8e58d7f5f3c138c779d552935bfd87.png)
Tidak ada komentar:
Posting Komentar